Louis La Minh Hoang

A study journey by Louis La Minh Hoang

recent posts

about

  • Math lesson

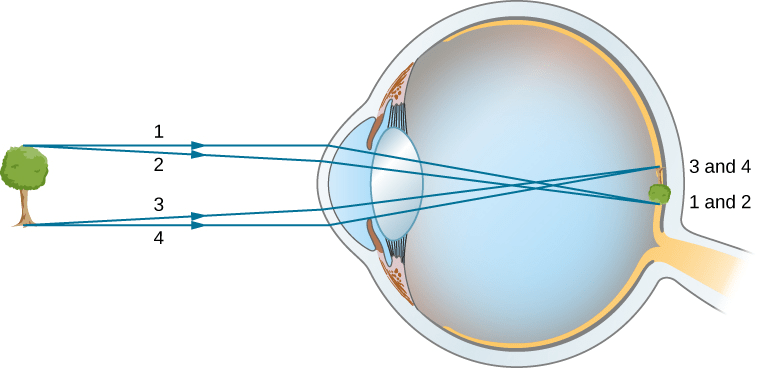
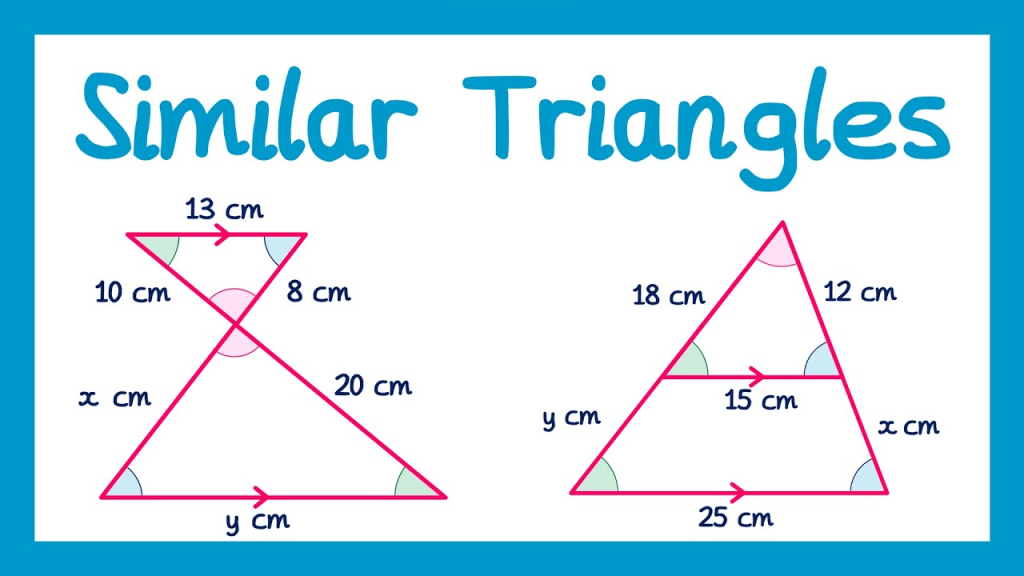
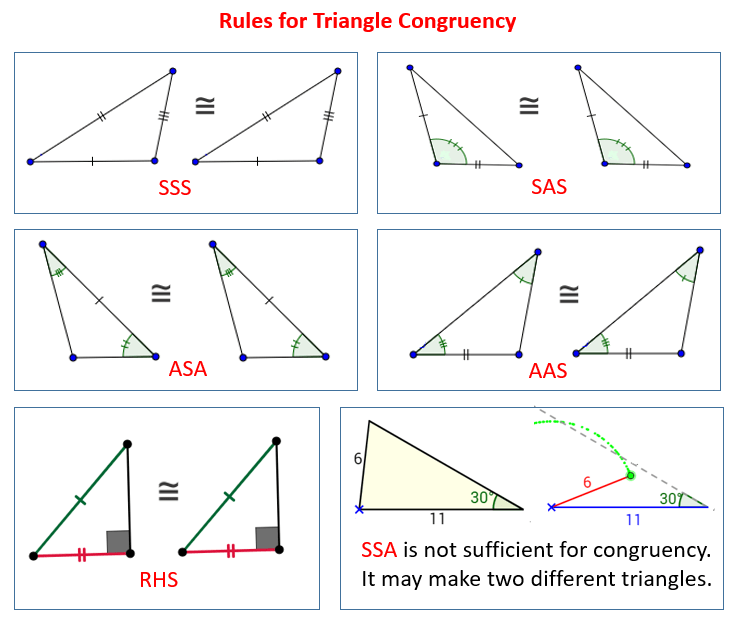
    Today’s math lesson was a full-circle return to the foundations of calculus, as we reviewed both differentiation and integration — the two pillars that support almost every advanced topic in mathematics. Even though I’ve learned them before, revisiting them together showed how closely connected they are and how powerful they become when used side by side.

    We started with differentiation, refreshing the core rules: power rule, product rule, quotient rule, and the chain rule. But instead of simply applying formulas, the focus was on understanding when and why each rule is used. We practiced identifying structures inside complicated expressions — spotting compositions, hidden products, and places where simplification can make the derivative cleaner. It was less about speed, more about strategy.

    Then we transitioned into integration, which always feels like the “reverse” puzzle to differentiation. We reviewed basic integrals, substitution, and recognizing patterns that match derivative rules. What made the lesson interesting was how integration suddenly became easier once the links between the two processes were emphasized. For example, identifying an expression that fits the derivative of a product or chain rule can immediately hint at the right integration method.

    A major part of the lesson was solving problems where both operations appear together — such as checking answers by differentiating integrals, or integrating to find displacement after differentiating a velocity function. Problems like these showed how differentiation and integration aren’t separate skills, but rather two tools that solve different sides of the same mathematical story.

    We also tackled a set of mixed practice questions that included simplifying before differentiating, integrating functions that look intimidating until you recognize a structure, and applying both techniques to real contexts like motion, area, and growth. These problems were challenging but satisfying, especially when both calculus tools worked together to complete a solution.

    Overall, this review felt like reinforcing the backbone of calculus. Differentiation and integration each have their own rules and tricks, but learning how they echo each other — and how one can undo or verify the other — really deepened my understanding. It was a solid, balanced refresher, and it made me feel more prepared for the harder calculus topics ahead.

  • Physics lesson on eyes

    Today’s physics lesson focused on the eye — but not in the biological sense. No anatomy, no retina cells, no rods or cones. Instead, we treated the eye purely as an optical system, a beautifully engineered arrangement of lenses, focal lengths, and image formation. It was all physics, all math, and surprisingly elegant.

    We approached the eye as a dynamic lens system whose focal length changes through accommodation. Instead of thinking about muscles and tissues, we analyzed this in the same way we study convex lenses: by considering how changing curvature alters focus, image position, and overall optical power. Treating the eye like a movable, adjustable lens suddenly made a lot of everyday experiences — reading, focusing far away, blurriness — feel like simple lens problems.

    One of the biggest parts of the lesson was understanding how the eye forms real, inverted images on the “screen,” which we simplified as the retina. We studied how altering the object distance affects the image distance and why the eye has to adjust its focal length instead of sliding the retina back and forth like a camera. This comparison made the physics behind vision feel almost mechanical — a system of distances, curvatures, and power adjustments.

    Then came the vision defects, again through a physics lens. We explored:

    • Myopia as the image forming in front of the retina → meaning the lens system’s power is too strong or the eyeball is too long.
    • Hyperopia as the image forming behind the retina → meaning the system’s power is too weak or the eyeball is too short.

    No biology — just image position and focal length mismatches.
    From there, it was all about correction using lenses: concave lenses for myopia, convex lenses for hyperopia, and the physics behind how they shift the image back onto the retina.

    We solved problems involving optical power (diopters), which linked directly to lens equations. For instance, determining the required optical power of glasses to correct a specific defect became a matter of combining image distances and focal lengths using the thin lens formula. It was surprisingly satisfying to see how the entire process reduces to straightforward, crisp mathematics when you strip away the anatomy.

    Another interesting part was the discussion on near point and far point — not as biological limits but as boundary distances determined by the maximum and minimum optical power the eye can produce. This sparked some challenging problems involving the range of accommodation, minimum focal length adjustments, and determining whether a person can read a book or see a distant sign.

    What made this lesson fun was how it turned something familiar — our own eyes — into a playground for lenses, rays, and equations. The focus wasn’t on memorizing facts, but on constructing a physical model that behaves exactly like a lens we’d use in any optical experiment. It was all about image formation, refraction behavior, and the math that determines what we see.

    A simple everyday act like looking at something suddenly felt like a series of optical calculations unfolding inside a lens system we all carry around. And studying it purely from the physics perspective made it feel both intuitive and deeply precise.

  • Computer science lesson, doing past IGCSE exams

    Today’s computer science session was all about putting my skills to the test — literally. Instead of reviewing notes or doing small exercises, I attempted a full IGCSE Computer Science practical-style exam, the one filled with algorithm design, pseudocode writing, logic tracing, and structured thinking. It was a long, intense session, but honestly one of the most productive I’ve had so far.

    I went through the entire paper and ended with a score of 58/60 on the main part. That felt satisfying, not because the questions were easy, but because I could see how much smoother my reasoning has become: loops feel natural, decisions feel predictable, and tracing algorithms no longer feels like guesswork. The only section I didn’t complete was the final 15-mark pseudocode design question — not because I couldn’t do it, but because time ran out. In a real exam, this would have been stressful, but in a practice session, it was the perfect reminder that logic alone isn’t enough; I also need speed and structure.

    But the most important part of the lesson wasn’t the score — it was the mistakes. I made two main ones, and both were the kind that can quietly steal marks if I’m not careful.

    The first was about defining parameters properly in functions and procedures. Sometimes I wrote headings too casually, forgetting that examiners expect very clear and formal definitions. It wasn’t that I didn’t understand parameters — it was the consistency and clarity that I slipped on. This is the kind of mistake that feels small until you realize the exam gives marks just for writing the heading correctly.

    The second mistake was related to validation in pseudocode, something that should be second nature by now. I understood what validation is supposed to do, but I rushed and wrote conditions that weren’t structured the way examiners like to see them. It reminded me that exam technique is its own skill: you can know what to do but still lose marks if you don’t present it cleanly and systematically.

    What I loved most about this lesson was how brutally honest it was. When you do real exam questions, you can’t hide behind theory anymore. Everything becomes exposed: your instincts, your habits, your weaknesses, and your strengths. And that’s exactly why this session was so valuable. It showed me what I already mastered — and what still needs sharpening.

  • Computer Science Lesson: Revising Pseudocode with IGCSE Past Questions

    In this computer science lesson, I revised writing pseudocode, with a strong focus on applying the rules correctly in IGCSE past exam questions. The lesson wasn’t about learning new syntax, but about sharpening accuracy, clarity, and exam technique.

    We went over the standard pseudocode conventions used in IGCSE, making sure structures like IF…THEN…ELSE, WHILE, REPEAT…UNTIL, and FOR loops were written clearly and logically. Small details mattered a lot, such as correct indentation, clear variable names, and making sure conditions were precise and unambiguous.

    Most of the practice involved breaking down wordy exam questions into step-by-step algorithms. This required careful reading to identify inputs, processes, and outputs before writing any pseudocode at all. Jumping straight into code often led to mistakes, so planning was just as important as writing.

    We also practiced using arrays, procedures, and functions where appropriate, especially in longer questions. Choosing when to use a loop or a procedure made the pseudocode more efficient and easier to understand, which is exactly what examiners look for.

    By working through real IGCSE past questions, this revision made the expectations very clear. Writing good pseudocode is less about being clever and more about being logical, structured, and precise. This lesson helped me improve not only my pseudocode skills, but also my overall problem-solving approach in computer science.

  • Community Project: Sharing Love – Reaching Out to Children in Flood-Affected Areas of Phu Yen and Gia Lai

    Each book given away carries a message. We hope that it will give students more learning opportunities and hope for the future!

  • My lesson on the inequalities theorems

    In this math lesson, I focused on complex inequalities through the use of specific and powerful inequality theorems, rather than trial-and-error or graphing alone. The emphasis was on recognizing structure and choosing the right theorem to simplify a difficult-looking problem.

    A major part of the lesson involved applying classic results such as the AM–GM inequality (revision only), Cauchy–Schwarz inequality, and basic forms of Jensen’s inequality in algebraic settings. These theorems allowed complicated expressions to be bounded cleanly, turning messy inequalities into elegant arguments. Understanding the equality cases was especially important, since they often determined the exact conditions for maximum or minimum values.

    We also worked with inequalities derived from completing the square and rearranging expressions into always-nonnegative forms. This approach made it possible to prove inequalities rigorously and to identify when an inequality holds for all real numbers versus only under certain constraints.

    Some problems required combining multiple ideas, such as using AM–GM to estimate part of an expression and then refining the result with algebraic manipulation. Others involved symmetry, where recognizing interchangeable variables simplified the inequality significantly.

    By the end of the lesson, complex inequalities felt less intimidating. With the right theorems and a clear strategy, even very difficult-looking inequalities became manageable. This lesson highlighted how inequality theory is not just about calculation, but about insight, structure, and mathematical elegance.

  • integration

    In this math lesson, I worked on integration, starting from the simple and foundational ideas before moving on to slightly more involved applications. The goal was to build a clear understanding of what integration actually represents, not just how to perform it mechanically.

    We began with basic integrals of common functions, treating integration as the reverse process of differentiation. This helped connect new ideas with what I had already learned, making the rules feel more natural rather than memorized. Understanding how powers change and why constants appear in the result was an important part of this stage.

    We also discussed the meaning of the constant of integration and why it must always be included when finding an indefinite integral. Instead of seeing it as an annoying extra symbol, we linked it to the idea that many different functions can have the same derivative.

    Simple applications were introduced as well, especially interpreting integration as the area under a curve. Even at this basic level, it required careful thinking about limits and the shape of graphs, reinforcing the connection between algebra and geometry.

    Although the content was introductory, this lesson laid the groundwork for more advanced integration techniques later on. By starting with simple cases and focusing on understanding, integration began to feel like a logical extension of differentiation rather than a completely new and separate topic.

  • similar triangle revision

    In this math lesson, I revised the topic of similar triangles, focusing on understanding the reasoning behind similarity rather than just applying ratios mechanically. Although the concept is familiar, the problems showed how powerful and subtle similarity can be in geometry.

    We reviewed the conditions for triangle similarity, and discussed how these guarantee that two triangles have the same shape even if their sizes are different. The emphasis was on recognizing similarity within complex diagrams, where the triangles are not immediately obvious and may be rotated, inverted, or partially overlapping.

    Many of the questions required setting up correct proportional relationships between corresponding sides. Choosing the right ratios was critical, as one mistake could break the entire solution. Some problems involved combining similarity with parallel lines, midpoints, or intersecting transversals, which added an extra layer of difficulty.

    We also used similar triangles to solve problems involving lengths, heights, and distances that could not be measured directly. These applications showed how similarity turns geometry into a powerful problem-solving tool rather than a purely theoretical idea.

    Overall, this revision reinforced how similar triangles form a bridge between visual geometry and algebraic thinking. When used carefully, they allow complex geometric situations to be simplified into clean, logical relationships that are both elegant and effective.

  • Triangle congruence revision

    In my math lesson, I focused on revising congruent triangles, reinforcing both the theory and the logical reasoning behind it. Even though this is a familiar topic, the revision showed that it is far more than just memorizing conditions — it is about building solid mathematical arguments.

    We reviewed the main criteria for triangle congruence and discussed why each condition is sufficient to guarantee that two triangles are exactly the same in size and shape. Rather than treating these as rules to apply blindly, we examined how each condition restricts a triangle’s structure until only one possible shape remains.

    The problems were more demanding than basic identification exercises. Many required multi-step proofs, where congruent triangles were used as an intermediate result to deduce further properties, such as equal angles, equal sides, or parallel lines. Choosing the correct pair of triangles to compare was often the hardest part of the problem.

    We also practiced applying congruence in geometric constructions and diagrams with minimal information, where careful observation and logical deduction were essential. A small oversight in labeling or angle matching could lead to an incorrect conclusion, so precision mattered a lot.

    By the end of the lesson, this revision strengthened my understanding of congruent triangles as a foundation of geometric reasoning. It reminded me that many complex geometry problems rely on these basic ideas, and mastering them makes advanced topics much clearer and more manageable.

  • SQL and databases

    In my computer science class, I studied databases and SQL, focusing on how data is stored, organized, and queried efficiently. Instead of seeing data as random information, this lesson emphasized structured thinking and logical design.

    We began with the fundamentals of databases, learning why tables are used and how rows and columns represent records and fields. A key part of the lesson was understanding primary keys and how they uniquely identify each record, ensuring data integrity and preventing duplication. We also looked at how relationships between tables work, especially when linking data across multiple tables.

    The main focus, however, was SQL (Structured Query Language). We practiced writing queries to retrieve specific data using commands such as Select, along with conditions to filter results. The challenge wasn’t memorizing syntax, but thinking clearly about what data was needed and how to express that request precisely in SQL.

    We also explored how SQL can be used to sort data, limit results, and perform basic calculations. Some tasks required combining multiple conditions, which demanded careful logical reasoning to avoid errors or unintended results. These exercises showed how powerful SQL can be when used correctly, even with relatively simple commands.

    Overall, this lesson made databases feel practical and essential. Learning SQL improved my ability to think systematically, break problems into smaller steps, and work with large sets of data efficiently — skills that are increasingly important in computer science and real-world applications.