Louis La Minh Hoang

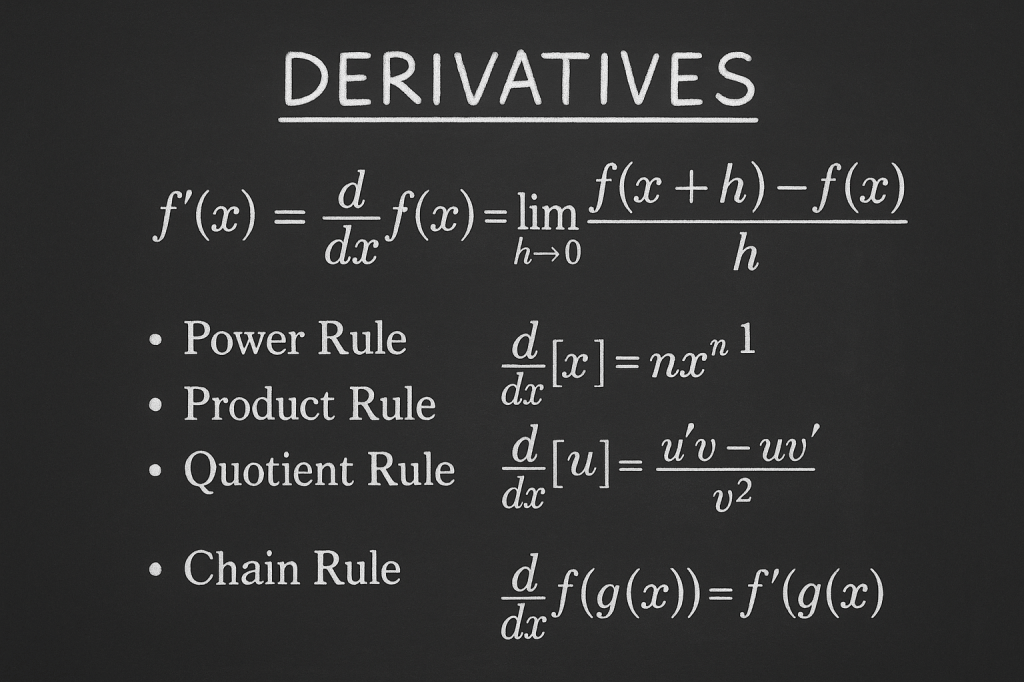
In today’s extra math class, we revisited derivatives, something I’d already learned before in another class — but this time, we went more in-depth and connected all the concepts together. At first, we reviewed the basics: understanding a derivative as the instantaneous rate of change or the slope of a tangent line at any point on a curve. It’s like zooming in infinitely close on a graph and seeing how fast it’s rising or falling right there.

After warming up with simple rules, like the power rule (d/dx[xn]=nxn−1d/dx[x^n] = nx^{n-1}d/dx[xn]=nxn−1) and basic derivatives of constants and linear terms, we got into more detailed rules — the product rule, quotient rule, and chain rule. These rules make it possible to handle complex composite functions, where terms are multiplied or nested inside each other. It was actually satisfying to see how all these separate pieces fit together logically.

Then we reached the second derivative — which goes a level deeper. While the first derivative tells you the rate of change, the second derivative shows how that rate itself changes. In simpler terms, it’s like checking whether your function is curving upwards or downwards. We talked about concavity, inflection points, and how the second derivative helps determine whether a point on a curve is a maximum, minimum, or a point where the curve changes direction.

We also did several practice problems, like differentiating polynomials, rational functions, and even a few that needed multiple rules at once. The best part was realizing how derivatives can describe real-world behaviors — like acceleration, optimization, and motion — and how the math we do on paper actually explains how things move and change in reality.

Overall, even though this wasn’t my first time learning derivatives, this session helped me understand the structure behind them — not just how to do the steps, but why each rule works. And going all the way to the second derivative really made me appreciate how powerful calculus can be once you start connecting everything together.