Louis La Minh Hoang

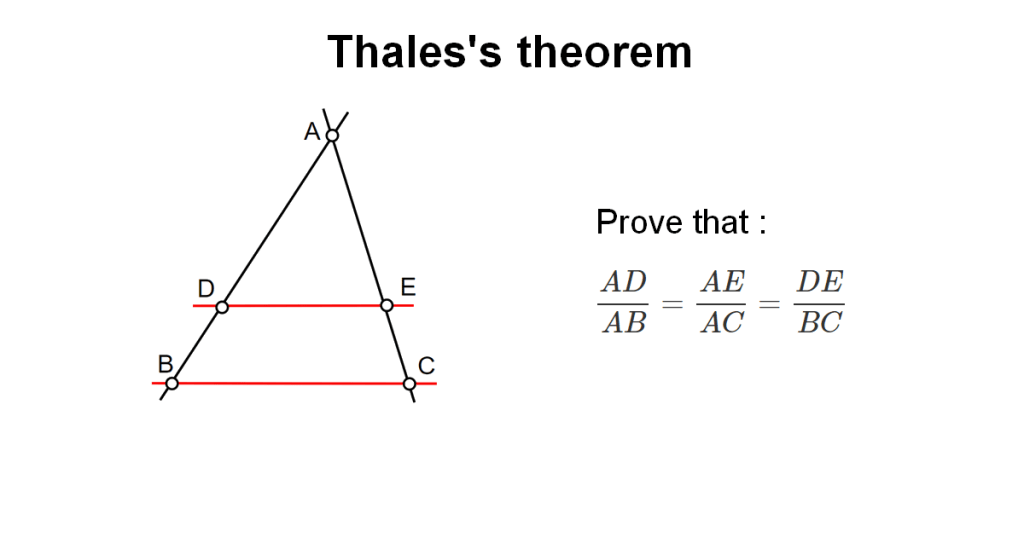
Today’s math lesson was all about going back to Thales’ Theorem — not the circle version, but the one about ratios in triangles when a line is drawn parallel to one of the sides. It might sound simple at first, but once you start solving the advanced problems, you realize how much geometry, algebra, and logic this theorem actually holds.

That single theorem connects everything — it’s the foundation of similar triangles, ratios, and proportional reasoning.

In class, we didn’t just apply it to easy cases. We went through complex geometry problems where multiple parallel lines divided triangles into smaller parts, and we had to find unknown lengths using proportion chains. Some questions even mixed in algebraic expressions, requiring careful setup and substitution to find exact segment ratios.

What made this lesson advanced wasn’t the formula itself — it was how it was used. We had to think logically about which triangles were similar, how the sides corresponded, and why the ratios remained consistent. It’s one of those topics where you can’t just memorize; you have to see the relationships and understand the geometry behind them.

By the end, I was able to solve some really tricky problems where Thales’ Theorem was the key that unlocked everything. It’s amazing how something that looks so simple — a few parallel lines — can lead to such deep and elegant mathematical reasoning.

In conclusion, today’s class reminded me that geometry isn’t about drawing shapes; it’s about finding hidden relationships. And Thales’ Theorem? It’s one of the most powerful tools for doing exactly that.