Louis La Minh Hoang

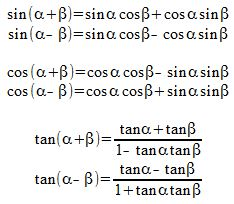
Today’s math class took trigonometry to a whole new level — the advanced world of compound angles, where we learned how to work with expressions like sin(a + b), cos(a + b), and tan(a + b). It wasn’t just about memorizing formulas — it was about understanding why they work and how they’re used to simplify complex geometric and algebraic problems.

We started by deriving the formulas from the unit circle and right triangle geometry, exploring how the relationships between sine, cosine, and tangent extend when two angles are combined.

These weren’t just shown as facts — we actually worked through the reasoning behind them, step by step.

Then came the real challenge — applying these formulas to non-standard problems. We solved equations where angles weren’t nice and clean, and sometimes had to convert between degrees and radians mid-solution. Some problems involved finding unknowns in triangles or proving trigonometric identities that looked terrifying at first glance but unraveled neatly with the right substitution.

What made it “super advanced” wasn’t just the formulas — it was how layers of trigonometry, geometry, and algebra came together. We even used these formulas to simplify expressions for wave functions and rotations, which made the math feel almost like physics in disguise.

In conclusion, today’s trigonometry session showed me the true beauty of math — how complex expressions can simplify perfectly when you understand their structure. The compound angle formulas aren’t just random identities; they’re the backbone of advanced trigonometric reasoning — elegant, powerful, and deeply satisfying when everything clicks.