Louis La Minh Hoang

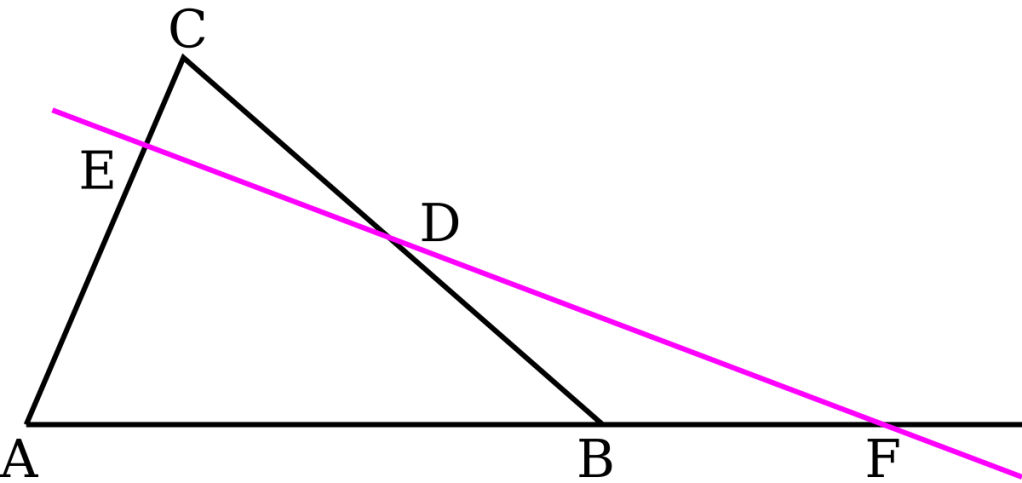
Today’s math lesson was all about one of the more elegant and lesser-known theorems in geometry — Menelaus’ Theorem. It’s not as famous as Pythagoras or Thales, but it’s a powerful tool for solving problems involving ratios in triangles and transversals. And honestly, it felt like uncovering a hidden trick that makes complicated geometry suddenly make sense.

We started with the theorem’s core idea: when a line (a transversal) cuts across the sides of a triangle (or their extensions), the product of three ratios equals 1 . And once you understand why it works, it opens up a whole new way to tackle geometry problems that involve proportionality and collinearity.

But it didn’t stop there. The real challenge came when applying Menelaus’ Theorem to complex figures — especially those involving multiple transversals or extended sides. It required sharp reasoning and precise ratio manipulation, not just memorization. The teacher pushed us to understand why each ratio is set up the way it is, and how the theorem connects to Ceva’s Theorem, its “dual” in geometry.

The best part? Seeing how Menelaus’ Theorem ties together geometry and algebra. Every step felt like balancing logic and calculation — a beautiful blend of precision and insight.

In conclusion, today’s lesson reminded me that geometry isn’t just about shapes and lines; it’s about relationships — hidden connections waiting to be discovered. And Menelaus’ Theorem? It’s one of those keys that unlocks deeper geometric reasoning.