Louis La Minh Hoang

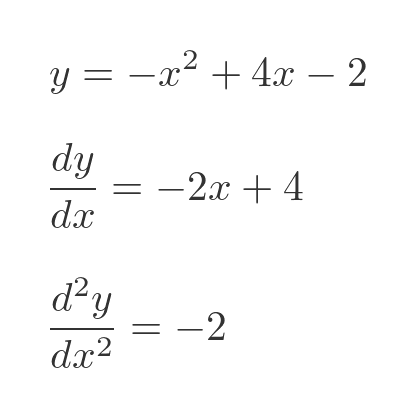
Today’s math session was all about advanced differentiation — not just finding derivatives, but truly understanding how to use them. It felt less like mechanical computation and more like decoding the behavior of functions.

We began with a quick revision of basic differentiation rules — product, quotient, and chain rules — just to warm up. But soon, we ventured into the advanced zone: second derivatives, curve sketching, and inflection analysis. It’s fascinating how one more layer of differentiation can reveal so much more about a function’s behavior.

The second derivative isn’t just “the derivative of a derivative.” It’s a window into curvature, helping us see how fast a slope changes and whether a graph bends upward or downward. We practiced identifying concavity, locating inflection points, and interpreting them geometrically.

But what made today’s lesson really advanced was the application part. We used first and second derivatives together to solve real-world optimization problems, like finding minimal surface areas or maximum efficiency points. Some problems involved implicit differentiation and parametric equations, which demanded careful step-by-step reasoning — one mistake in a chain rule, and the entire structure could collapse.

The best part was exploring how second derivatives link back to motion and physics — understanding acceleration as the derivative of velocity, and curvature as the geometry of motion. It connected pure math to the physical world in such a powerful way.

By the end, the revision came full circle: what began as a refresher turned into a deep dive into how calculus shapes everything — from graphs to growth, from speed to structure.

It wasn’t easy, but it was deeply satisfying. Advanced derivation isn’t about memorizing formulas — it’s about seeing the soul of change itself.