Louis La Minh Hoang

Today’s physics revision focused on plane mirrors, but not in the simple way we learned before. This session pushed everything into advanced geometric reasoning, where every reflection became a precise angle problem rather than just a quick sketch. It felt like a mixture of physics and high-level geometry combined into one challenge.

We began by reviewing the basic rules of reflection, but the moment we started solving questions, everything became much more demanding. Instead of casually drawing rays, we had to work with exact angle relationships, using alternate interior angles, angle sums, and careful constructions. A single reflection wasn’t just “angle in equals angle out” anymore — it became a full geometric argument.

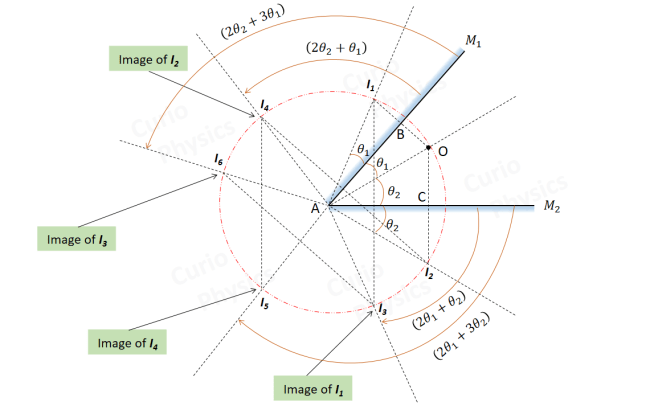
The real difficulty appeared when dealing with two or three mirrors positioned at unusual angles. A ray reflecting from one mirror could hit another at a completely different orientation, and the only way to track it correctly was through step-by-step geometric reasoning. Each reflection had to be justified using triangle constructions, angle chasing, and similar triangle reasoning. Finding the final image point meant repeatedly reflecting the object across different mirror lines, building a chain of reflected points that followed strict geometric rules.

We also explored situations where two mirrors face each other and create multiple images. Instead of memorizing formulas, we worked out why those images appear by understanding the repeating angles formed between successive reflections. It was surprising to see how something that looks simple in real life can turn into a full mathematical pattern once you dig into the reflections properly.

The hardest questions involved mirrors placed at awkward angles like 37° or 53°. In these cases, even one small mistake in drawing or angle calculation would lead to a completely wrong result. Everything depended on accuracy and logical thinking, not memorization.

By the end of the lesson, I realized that revising plane mirrors at this advanced level reveals how deep the topic actually is. Light follows perfect geometry, and when we trace it precisely, the entire problem becomes a beautiful, challenging structure of angles and symmetry. Even the simplest mirror can turn into a serious test of mathematical thinking when approached at this level.