Louis La Minh Hoang

My geometry lesson today focused on two powerful tools that appear constantly in Olympiad-level problems: Ceva’s Theorem and the Angle Bisector Theorem. Even though both theorems look clean and simple at first, applying them correctly requires a strong understanding of ratios, triangle structures, and how lines interact inside a triangle.

We started with the Angle Bisector Theorem, which explains how an internal angle bisector splits the opposite side into segments proportional to the adjacent sides. It sounds easy, but using it efficiently means recognizing bisectors hidden inside complicated diagrams. Many problems disguised the bisector behind multiple constructions, forcing me to analyze side lengths, identify equal angles, and express everything in ratio form before finding the missing segment.

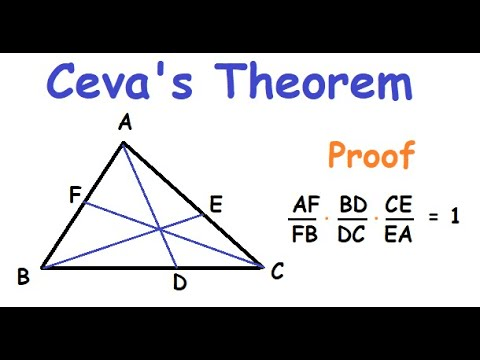
After that, we moved to Ceva’s Theorem, which connects three concurrent lines in a triangle using a multiplicative ratio condition. At first glance it seems abstract, but once we started solving problems, I saw how powerful it is. Instead of guessing intersection points or trying random similarity arguments, Ceva let me confirm immediately whether three cevians could meet at a single point. Working backward from concurrency also helped solve problems where one cevian’s ratio was unknown.

The hardest part wasn’t the theorems themselves, but the way they were used in combination. Some problems required applying the Angle Bisector Theorem first to find ratios, then plugging those ratios into Ceva’s Theorem to check concurrency. Others needed rearranging Ceva’s formula or converting segments into proportional expressions. Each challenge felt like piecing together a puzzle of ratios and angles.

By the end of the lesson, both theorems felt far more natural. Instead of relying on guesswork, I could approach geometry problems with precise ratio tools and a more structured way of proving concurrency and segment divisions. These theorems are definitely essential for more advanced geometry, and I’m starting to appreciate how elegant and powerful they can be when used effectively.