Louis La Minh Hoang

My physics lesson today went even further into the world of lenses, pushing past the basic ray diagrams and into the full mathematical framework behind how images form. Instead of just drawing the principal rays, we focused on the core formulas, how to apply them correctly, and how to handle tricky problem variations that appear in advanced exams.

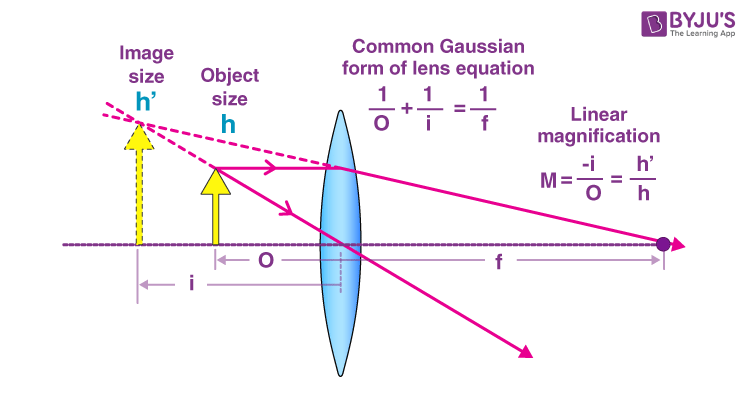
We started with the fundamental lens formula, which connects the object distance $u$u, image distance $v$v, and focal length. But instead of just plugging in numbers, we broke down when the formula works, how to choose the correct sign conventions, and how to interpret the final image (real/virtual, inverted/upright, enlarged/diminished). Knowing how to apply the signs was honestly the biggest challenge, since a single mistake flips the entire answer.

From there, we moved into magnification, which is another crucial formula. We practiced questions combining both formulas, especially ones where you don’t know the image distance and must calculate it from the focal length. These usually involve multiple steps, and I had to carefully track each value to avoid errors.

We also reviewed the properties of converging vs diverging lenses, especially how diverging lenses always produce virtual, upright, and reduced images. But the tricky part was solving mixed-lens systems, where one lens forms an image that becomes the object for the second lens. Drawing those diagrams while applying the formulas correctly was absolutely the hardest part, because one wrong arrow or sign changes everything.

One interesting part of the lesson was analyzing the limiting cases, like when the object is placed exactly at the focal point. In that case, the image distance becomes infinite, and the rays emerge parallel. Understanding why that happens physically made the formula feel much more intuitive.

By the end, I realized how much depth lenses actually have once you go beyond the simple drawings. Using formulas like the lens equation and magnification, applying sign conventions, and combining multiple lenses all turn image formation into a genuine mathematical challenge. But now I feel much more confident tackling complex lens problems, especially the ones that require both geometry and algebra to get to the final answer.