Louis La Minh Hoang

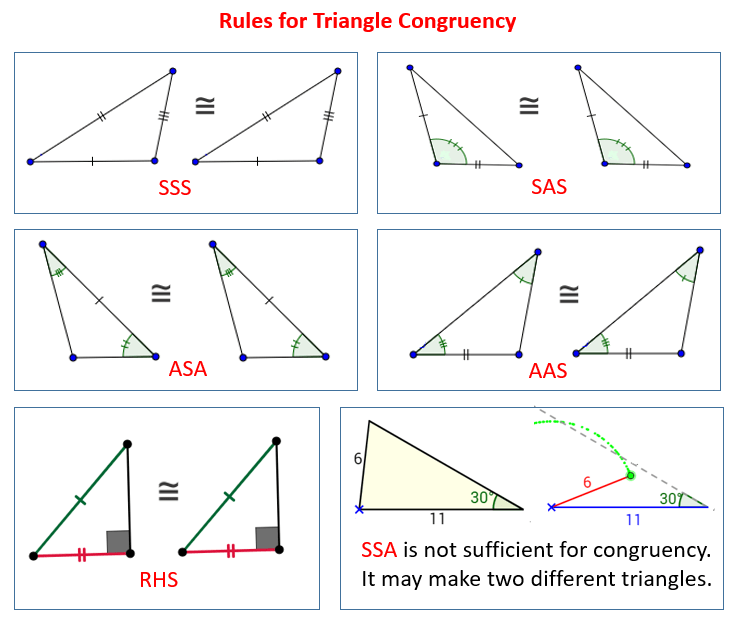
In my math lesson, I focused on revising congruent triangles, reinforcing both the theory and the logical reasoning behind it. Even though this is a familiar topic, the revision showed that it is far more than just memorizing conditions — it is about building solid mathematical arguments.

We reviewed the main criteria for triangle congruence and discussed why each condition is sufficient to guarantee that two triangles are exactly the same in size and shape. Rather than treating these as rules to apply blindly, we examined how each condition restricts a triangle’s structure until only one possible shape remains.

The problems were more demanding than basic identification exercises. Many required multi-step proofs, where congruent triangles were used as an intermediate result to deduce further properties, such as equal angles, equal sides, or parallel lines. Choosing the correct pair of triangles to compare was often the hardest part of the problem.

We also practiced applying congruence in geometric constructions and diagrams with minimal information, where careful observation and logical deduction were essential. A small oversight in labeling or angle matching could lead to an incorrect conclusion, so precision mattered a lot.

By the end of the lesson, this revision strengthened my understanding of congruent triangles as a foundation of geometric reasoning. It reminded me that many complex geometry problems rely on these basic ideas, and mastering them makes advanced topics much clearer and more manageable.