Louis La Minh Hoang

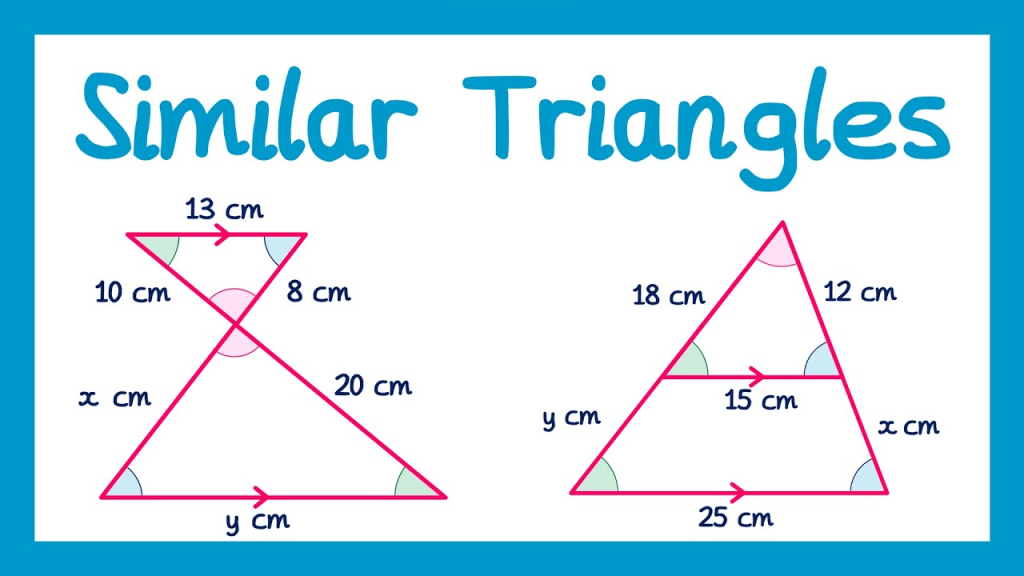
In this math lesson, I revised the topic of similar triangles, focusing on understanding the reasoning behind similarity rather than just applying ratios mechanically. Although the concept is familiar, the problems showed how powerful and subtle similarity can be in geometry.

We reviewed the conditions for triangle similarity, and discussed how these guarantee that two triangles have the same shape even if their sizes are different. The emphasis was on recognizing similarity within complex diagrams, where the triangles are not immediately obvious and may be rotated, inverted, or partially overlapping.

Many of the questions required setting up correct proportional relationships between corresponding sides. Choosing the right ratios was critical, as one mistake could break the entire solution. Some problems involved combining similarity with parallel lines, midpoints, or intersecting transversals, which added an extra layer of difficulty.

We also used similar triangles to solve problems involving lengths, heights, and distances that could not be measured directly. These applications showed how similarity turns geometry into a powerful problem-solving tool rather than a purely theoretical idea.

Overall, this revision reinforced how similar triangles form a bridge between visual geometry and algebraic thinking. When used carefully, they allow complex geometric situations to be simplified into clean, logical relationships that are both elegant and effective.