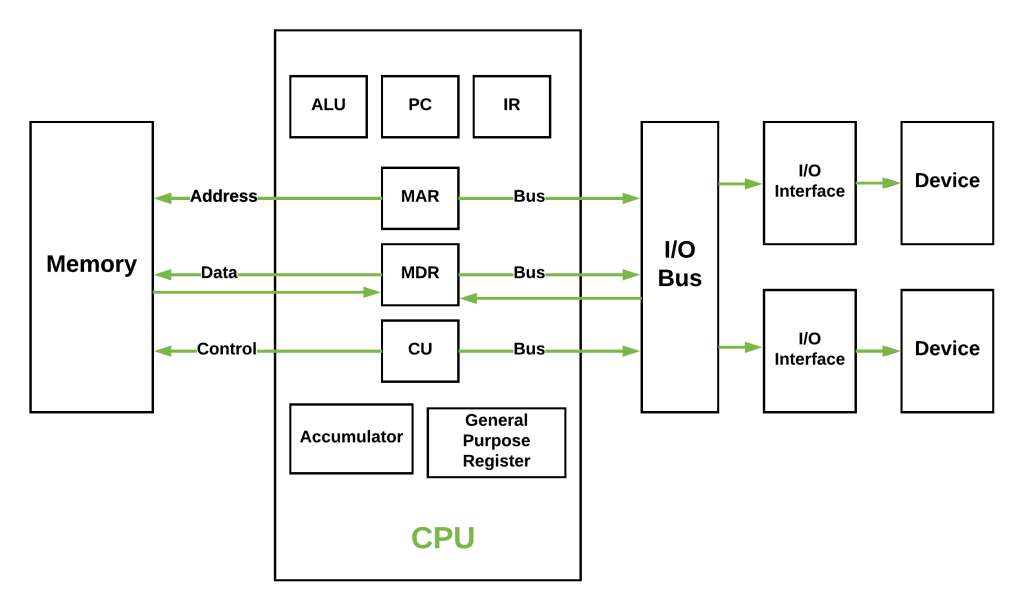
In my computer science lesson, I focused on revising input and output devices, which are essential for how a computer communicates with the outside world. Even though this topic is familiar, revisiting it helped me understand more clearly how hardware and users interact through data flow.
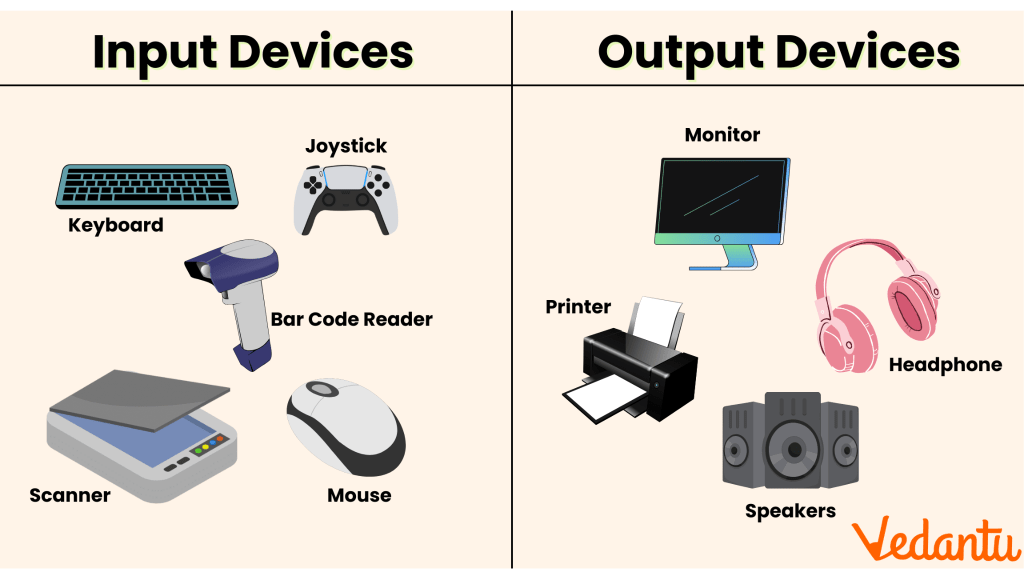
We started with input devices, which allow users to send data and instructions into the computer system. Common examples include the keyboard, mouse, scanner, microphone, and sensors. Instead of just naming them, we discussed what type of data each device inputs, such as text, images, sound, or control signals. This made it easier to understand why different devices are designed the way they are and how they are used in different situations.
Then we moved on to output devices, which present processed data back to the user. Devices like monitors, printers, speakers, and projectors were analyzed not only by their function, but also by their output type — visual, audio, or physical (like printed documents). We also looked at how resolution, refresh rate, and output quality affect the user experience.
An important part of the lesson was understanding the input–process–output cycle. Input devices provide raw data, the CPU processes it, and output devices display the result. Seeing input and output as part of a complete system rather than isolated components made the topic much clearer.
Overall, this revision strengthened my understanding of how computers interact with users and the real world. Input and output devices may seem simple, but they are critical to making computers practical and usable.