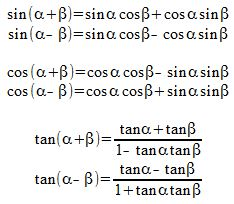Louis La Minh Hoang

A study journey by Louis La Minh Hoang

recent posts

about

  • Trigonometry revision

    Today I spent my study session revising trigonometry, and it turned into a solid mix of recalling key identities, applying angle relationships, and solving problems that required careful reasoning rather than quick memorization. Even though I’ve learned these ideas before, revisiting them with more experience made everything connect more smoothly.

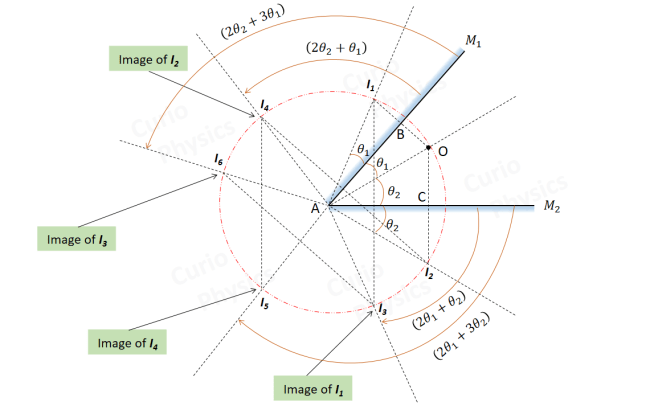
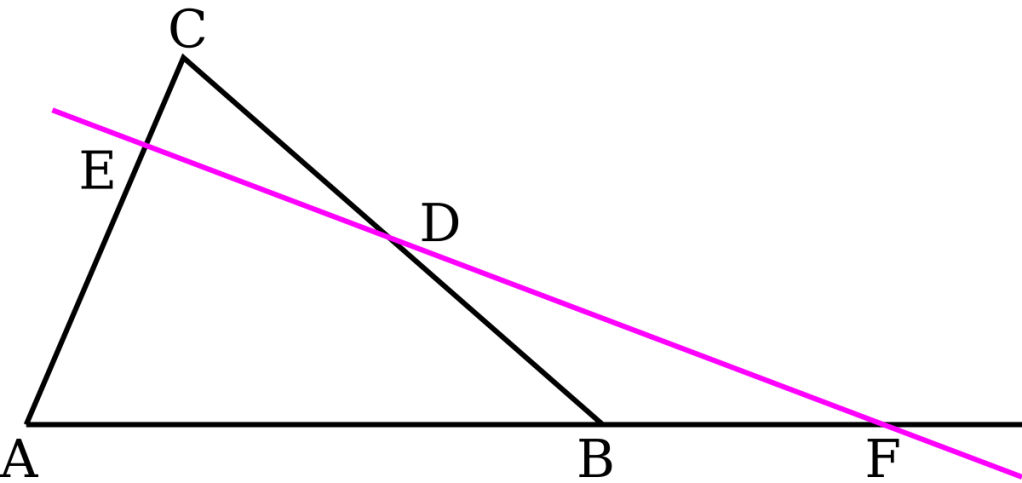
    I revised the sine rule and cosine rule, paying attention to when each one is appropriate. Some questions required switching between them depending on which sides or angles were known. The cosine rule was especially important in finding unknown sides in scalene triangles, and it was interesting to see how much geometry depends on that one identity.

    I also reviewed trigonometric identities and angle transformations, simplifying expressions, and complementary relationships. These appeared in several past-paper style questions, and solving them correctly depended on remembering the sign changes and quadrant behavior.

    The most challenging problems involved combining multiple skills — using an identity, substituting values, forming equations, and sometimes solving for angles that weren’t straightforward. These questions reminded me how precise trigonometry can be: one small mistake in rearranging, and the answer changes completely.

    By the end, the revision helped reinforce both the computational side of trigonometry and the deeper logic behind it. Working through these problems made the topic feel more structured and predictable, and I could see clearly how each formula fits into the bigger picture of geometry and algebra.

    Today’s trigonometry revision wasn’t just practice — it was a step toward mastering the entire framework.

  • Another lesson + revision on derivation

    Today I continued my work on differentiation, building on everything I’ve studied so far while sharpening my understanding through deeper revision. Even though I already know the basic rules, this session pushed me to apply them more fluently and to connect different ideas together in a more advanced way.

    I started by reviewing the fundamental techniques — power rule, product rule, quotient rule, and chain rule — but instead of doing simple textbook examples, I focused on problems that combined several rules at once. This kind of revision forces me to think carefully about the structure of each function, especially when the expression contains nested brackets or multiple layers of composition.

    Then I moved into second derivatives again, this time using them to analyse the shape of graphs. I practised identifying turning points, determining their nature, and explaining why a function is concave up or concave down in specific intervals. It wasn’t just mechanical differentiation; it was about interpreting what the derivatives really meant. Working out where the gradient increases or decreases helped make the graph feel alive and logical.

    I also revised differentiation in the context of real applications — rate of change questions and optimization problems. These problems required more thought than direct calculations. For example, finding maximum values or minimum surface areas meant setting up the function properly, identifying the correct variable to differentiate, and then proving that the critical point was the correct solution. This part of the revision helped me see how differentiation connects directly to real-world ideas.

    Finally, I solved several advanced-style problems involving implicit differentiation and situations where functions were defined in terms of each other. These questions were challenging but satisfying, especially when the final result depended on maintaining careful steps and avoiding small errors.

    Overall, today’s session strengthened both my confidence and my technique. Continuing the study and revision of differentiation helped me see how all the rules and concepts support each other, and how each level of understanding builds toward more complex and elegant mathematics.

  • Radiation revision

    Today’s physics revision was all about radiation, but instead of treating it as a basic review, I focused on truly understanding the behaviour, patterns, and reasoning behind every concept. Radiation is a major part of IGCSE physics, and revisiting it with a sharper mindset made everything feel clearer and more connected.

    I began with the three main types of radiation — alpha, beta, and gamma — not just memorizing their properties, but examining why they behave differently. Alpha particles are massive and highly ionising because of their size and charge. Beta particles are fast-moving electrons that can travel farther. Gamma rays are pure electromagnetic waves with no mass, making them extremely penetrating. Seeing how structure influences behaviour made these differences feel logical rather than like random facts.

    Next, I reviewed penetration and ionisation, understanding how radiation interacts with matter. Instead of simply recalling which material blocks which type, I thought about how each particle loses energy, how ionisation causes damage, and why thicker or denser materials stop certain particles more effectively. This made radiation safety — shielding, exposure, and distance — make a lot more sense.

    I also revised half-life, not by just solving basic questions, but by analysing decay curves and explaining why radioactive activity decreases the way it does. Working through half-life graphs helped me understand how predictable radioactive decay is, even though the exact moment for any individual nucleus is random.

    The most challenging part of the revision came from past-paper style problems. These were not simple recall questions; they demanded reasoning. Some required identifying an isotope based on decay patterns. Others involved interpreting radiation readings, working out shielding effects, or explaining how contamination differs from irradiation. Each question forced me to think carefully about the physical process behind the answer.

    By the end of the session, I realized that radiation isn’t just about particles being emitted. It’s a balance of physics, probability, and structure. Revising it at a deeper level made the entire topic feel more intuitive and gave me more confidence in tackling advanced-style exam problems.

    Today’s revision wasn’t just refreshing old knowledge — it was strengthening my understanding of how radiation truly works.

  • Chemistry- revision on metals

    Today’s chemistry study session was a full revision of metals, but instead of treating it as a simple recap, I approached it with deeper understanding and more advanced reasoning. Metals are one of the most important topics in IGCSE chemistry, and going through everything again helped me see how all the ideas connect.

    I began with the properties of metals, revisiting why they conduct electricity, why they’re malleable, and how metallic bonding creates a structure where positive ions sit in a “sea” of delocalized electrons. What felt simple before now made much more sense when I linked these properties directly to their atomic structure.

    I reviewed the reactivity series, not just memorizing the order but understanding why certain metals react more vigorously than others. The idea of electron loss and ease of oxidation helped explain why metals like potassium and sodium react explosively, while copper barely reacts at all. This deeper view made the whole reactivity series feel logical instead of random.

    Then I went through the methods of extracting metals from ores, such as using electrolysis for reactive metals and carbon reduction for less reactive ones. I focused on the reasoning behind each method — how the position in the reactivity series determines the extraction process, and why different ores need different treatments. This part connected chemistry to real industrial processes, which made it more interesting.

    I also revised the reactions of metals with acids, water, and oxygen, paying attention to the patterns in products and the conditions needed for each reaction. Understanding why certain metals form specific ions or oxides helped me solve the more complex questions in past papers.

    Finally, I practiced advanced questions involving metal displacement, redox reactions, and identifying unknown metals through reasoning rather than memorization. These problems required careful thought, comparing reactivity, and predicting outcomes step by step.

    Overall, this revision session helped me turn scattered knowledge into a clear system. Metals aren’t just a list of facts — they form an entire framework in chemistry, connecting bonding, reactivity, extraction, and real-world applications. Studying them again made everything sharper and more satisfying

  • physics – graph

    Today’s physics lesson was all about graphs, but not the basic “read the value from the axis” type. We studied the deeper, more advanced side of interpreting graphs in physics — the kind that appears in electricity, pressure, heat, and motion. What made this session challenging wasn’t the content itself, but the level of analysis required to solve problems accurately.

    We started with speed–time and distance–time graphs, but instead of simple interpretations, we focused on how the shape of the graph reveals the exact behavior of an object. A straight line meant constant acceleration, a curve meant changing acceleration, and the area under the graph gave distance. The challenge came from unusual graphs: sudden jumps, piecewise curves, and sections that required integrating or comparing slopes carefully.

    Next, we worked with pressure–volume graphs, especially in contexts like gases and fluids. Here, the relationships weren’t linear, so solving problems required understanding how curves behave. A slight change in the graph’s steepness could completely alter the relationship. Many questions asked for energy changes or work done, which meant analyzing areas under curves rather than relying on formulas alone.

    Then came electricity graphs — current–time, voltage–time, and charge graphs. The key here was understanding that the graph’s gradient or area corresponded to physical quantities. Current–time graphs required integrating to find charge. Voltage–time graphs revealed potential differences that changed with time, especially in circuits involving components like capacitors. These problems required thinking in terms of relationships, not memorized rules.

    We also studied heating and cooling curves, where the graph’s flat sections represented phase changes. Instead of simply identifying the plateau, we had to reason about energy input, latent heat, and specific heat capacity, linking the graph’s shape to the physical behavior happening at each temperature region.

    Throughout the lesson, the biggest focus was on strategies rather than formulas. The teacher emphasized looking at three elements: the slope, the area under the curve, and the overall trend. Solving a graph problem meant translating a visual change into a physical explanation. Instead of just calculating, we had to justify why the graph looked the way it did and what that meant physically.

    By the end of the session, I realized how powerful graphs really are in physics. They don’t just show numbers; they reveal the entire story of a physical process. Understanding how to read them deeply is one of the most important skills in the subject, and today’s advanced practice made that clearer than ever.

  • Physics. plane mirror and images

    Today’s physics revision focused on plane mirrors, but not in the simple way we learned before. This session pushed everything into advanced geometric reasoning, where every reflection became a precise angle problem rather than just a quick sketch. It felt like a mixture of physics and high-level geometry combined into one challenge.

    We began by reviewing the basic rules of reflection, but the moment we started solving questions, everything became much more demanding. Instead of casually drawing rays, we had to work with exact angle relationships, using alternate interior angles, angle sums, and careful constructions. A single reflection wasn’t just “angle in equals angle out” anymore — it became a full geometric argument.

    The real difficulty appeared when dealing with two or three mirrors positioned at unusual angles. A ray reflecting from one mirror could hit another at a completely different orientation, and the only way to track it correctly was through step-by-step geometric reasoning. Each reflection had to be justified using triangle constructions, angle chasing, and similar triangle reasoning. Finding the final image point meant repeatedly reflecting the object across different mirror lines, building a chain of reflected points that followed strict geometric rules.

    We also explored situations where two mirrors face each other and create multiple images. Instead of memorizing formulas, we worked out why those images appear by understanding the repeating angles formed between successive reflections. It was surprising to see how something that looks simple in real life can turn into a full mathematical pattern once you dig into the reflections properly.

    The hardest questions involved mirrors placed at awkward angles like 37° or 53°. In these cases, even one small mistake in drawing or angle calculation would lead to a completely wrong result. Everything depended on accuracy and logical thinking, not memorization.

    By the end of the lesson, I realized that revising plane mirrors at this advanced level reveals how deep the topic actually is. Light follows perfect geometry, and when we trace it precisely, the entire problem becomes a beautiful, challenging structure of angles and symmetry. Even the simplest mirror can turn into a serious test of mathematical thinking when approached at this level.

  • My study on electromagnetic and magnetic field.

    Today’s physics lesson took me deep into one of the most mind-bending topics yet — electromagnetism. It’s strange how something completely invisible can be so perfectly predictable through mathematics.

    We began with the basics of magnetic fields, revisiting how current-carrying wires create circular field lines, and how solenoids act like controllable magnets. But soon, we dove into the advanced part — how changing magnetic fields induce electric currents, and how that interplay builds the very foundation of our technology.

    The equations weren’t simple — they required not just algebra, but a strong geometric sense. Understanding the right-hand rule, field direction, and how flux changes across surfaces demanded precise visualization. We explored Faraday’s Law, Lenz’s Law, and how negative signs reveal nature’s tendency to resist change.

    Then came the thrilling part: the electromagnetic field — the unification of electricity and magnetism. We analyzed how a moving charge produces both electric and magnetic components, and how together they form Maxwell’s masterpiece — the electromagnetic wave. We didn’t just study the formulas; we examined how they behave, how they ripple through space at the speed of light, binding electricity and magnetism into one elegant theory.

    Our teacher challenged us with complex problems — not just plug-in calculations, but ones that required deep physical intuition: predicting the direction of induced currents, analyzing forces on moving conductors, and reasoning through three-dimensional field interactions.

    By the end, I realized — electromagnetism isn’t just a chapter in physics. It’s the architecture of reality itself. Every light beam, every Wi-Fi signal, every heartbeat monitored by a sensor — all of it comes from these swirling, intertwined fields we can’t see, but can understand through pure reasoning and mathematics.

  • Second derivation revision

    Today’s math session was all about advanced differentiation — not just finding derivatives, but truly understanding how to use them. It felt less like mechanical computation and more like decoding the behavior of functions.

    We began with a quick revision of basic differentiation rules — product, quotient, and chain rules — just to warm up. But soon, we ventured into the advanced zone: second derivatives, curve sketching, and inflection analysis. It’s fascinating how one more layer of differentiation can reveal so much more about a function’s behavior.

    The second derivative isn’t just “the derivative of a derivative.” It’s a window into curvature, helping us see how fast a slope changes and whether a graph bends upward or downward. We practiced identifying concavity, locating inflection points, and interpreting them geometrically.

    But what made today’s lesson really advanced was the application part. We used first and second derivatives together to solve real-world optimization problems, like finding minimal surface areas or maximum efficiency points. Some problems involved implicit differentiation and parametric equations, which demanded careful step-by-step reasoning — one mistake in a chain rule, and the entire structure could collapse.

    The best part was exploring how second derivatives link back to motion and physics — understanding acceleration as the derivative of velocity, and curvature as the geometry of motion. It connected pure math to the physical world in such a powerful way.

    By the end, the revision came full circle: what began as a refresher turned into a deep dive into how calculus shapes everything — from graphs to growth, from speed to structure.

    It wasn’t easy, but it was deeply satisfying. Advanced derivation isn’t about memorizing formulas — it’s about seeing the soul of change itself.

  • Advance trigonometry

    Today’s math class took trigonometry to a whole new level — the advanced world of compound angles, where we learned how to work with expressions like sin(a + b), cos(a + b), and tan(a + b). It wasn’t just about memorizing formulas — it was about understanding why they work and how they’re used to simplify complex geometric and algebraic problems.

    We started by deriving the formulas from the unit circle and right triangle geometry, exploring how the relationships between sine, cosine, and tangent extend when two angles are combined.

    These weren’t just shown as facts — we actually worked through the reasoning behind them, step by step.

    Then came the real challenge — applying these formulas to non-standard problems. We solved equations where angles weren’t nice and clean, and sometimes had to convert between degrees and radians mid-solution. Some problems involved finding unknowns in triangles or proving trigonometric identities that looked terrifying at first glance but unraveled neatly with the right substitution.

    What made it “super advanced” wasn’t just the formulas — it was how layers of trigonometry, geometry, and algebra came together. We even used these formulas to simplify expressions for wave functions and rotations, which made the math feel almost like physics in disguise.

    In conclusion, today’s trigonometry session showed me the true beauty of math — how complex expressions can simplify perfectly when you understand their structure. The compound angle formulas aren’t just random identities; they’re the backbone of advanced trigonometric reasoning — elegant, powerful, and deeply satisfying when everything clicks.

  • Menelaus theorem

    Today’s math lesson was all about one of the more elegant and lesser-known theorems in geometry — Menelaus’ Theorem. It’s not as famous as Pythagoras or Thales, but it’s a powerful tool for solving problems involving ratios in triangles and transversals. And honestly, it felt like uncovering a hidden trick that makes complicated geometry suddenly make sense.

    We started with the theorem’s core idea: when a line (a transversal) cuts across the sides of a triangle (or their extensions), the product of three ratios equals 1 . And once you understand why it works, it opens up a whole new way to tackle geometry problems that involve proportionality and collinearity.

    But it didn’t stop there. The real challenge came when applying Menelaus’ Theorem to complex figures — especially those involving multiple transversals or extended sides. It required sharp reasoning and precise ratio manipulation, not just memorization. The teacher pushed us to understand why each ratio is set up the way it is, and how the theorem connects to Ceva’s Theorem, its “dual” in geometry.

    The best part? Seeing how Menelaus’ Theorem ties together geometry and algebra. Every step felt like balancing logic and calculation — a beautiful blend of precision and insight.

    In conclusion, today’s lesson reminded me that geometry isn’t just about shapes and lines; it’s about relationships — hidden connections waiting to be discovered. And Menelaus’ Theorem? It’s one of those keys that unlocks deeper geometric reasoning.